2025-06-03 ETH最新CMDP框架亮相，ANYmal四足机器人首次实现与人类羽毛球“过招”

作者：李鑫   出品：具身智能大讲堂

机器人与人类协作最为关键的问题在于如何突破物理约束，提升机器人系统的稳定性和安全性。近日苏黎世联邦理工学院机器人系统实验室提出了一套CMDP全新框架，该框架通过约束强化学习在减少约束违反、提升系统鲁棒性方面的明显优势，能够有效提升足式机器人在复杂环境中的运动性能。

研究人员将CMDP框架应用在ANYmal四足机器人，并实现了人机羽毛球对打交互的效果。目前该论文《Evaluation of Constrained Reinforcement Learning Algorithms for Legged Locomotion》已在《Science Robotics》发表。

CMDP框架研究目标与方法概述

足式机器人（如四足、六足机器人）因其能在复杂地形中灵活运动而备受关注。然而，传统基于模型的控制方法在处理高维动态系统时面临诸多挑战。深度强化学习作为一种数据驱动的控制技术，为足式机器人运动控制提供了新思路——通过智能体与环境的持续交互，逐步学习最优策略以最大化累积奖励。但在实际应用中，机器人必须严格遵守物理约束条件，例如关节速度限制、扭矩阈值等，以确保系统稳定性和安全性。

然而，当前多数深度强化学习研究在模型训练阶段未能充分考虑这些物理约束，导致实际应用时性能下降甚至引发安全隐患。例如，过度追求策略优化可能使机器人关节超出物理极限，造成机械损伤或失控。因此，如何在训练过程中有效整合物理约束，成为提升深度强化学习在机器人控制领域实用性的核心问题。

为了评估约束强化学习算法在足式机器人运动控制中的实际效果，特别是算法对物理约束的处理能力。研究人员采用了CMDP框架，将物理约束与奖励函数分离处理，通过比较五种一阶约束策略优化算法（P3O、PPO-Lagrangian、IPO、CRPO、FOCOPS），评估它们在模拟到现实转移中的表现。实验部分包括算法比较和机器人实验，以验证约束强化学习在减少约束违反、提升系统稳定性方面的有效性。

深度强化学习通过机器人与环境的交互，不断试错并优化策略，以最大化累积奖励。但在实际应用中，机器人必须满足物理约束（如关节扭矩限制、速度限制等），这些约束是确保系统安全与稳定的基础。

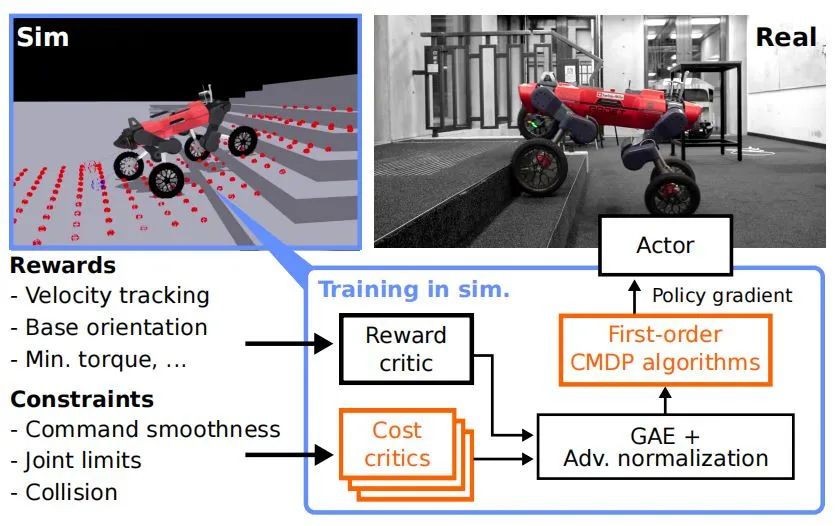
CMDP框架通过引入成本函数，将约束条件转化为优化目标的一部分，形成带约束的马尔可夫决策过程。在CMDP中，机器人不仅需最大化累积奖励，还需确保累积成本不超过预设阈值。这一框架为处理物理约束提供了数学工具，使算法能在约束范围内寻找最优策略。

五种一阶约束策略优化算法比较

研究人员比较了五种一阶约束策略优化算法，这些算法通过不同的方式将约束条件纳入策略优化过程，实现约束满足与奖励最大化的平衡。

P3O（惩罚近端策略优化）：

通过惩罚项将约束违反纳入目标函数，并使用裁剪替代目标（CLIP）稳定训练。该方法简单直观，但在处理复杂约束时可能不够灵活。

PPO-Lagrangian（拉格朗日松弛法）：

利用拉格朗日松弛将约束问题转化为无约束优化，通过迭代原始-对偶方法求解。该方法理论收敛性较好，但实际应用中需要仔细调整参数。

IPO（内点策略优化）：

受内点法启发，在接近约束边界时通过对数障碍函数施加无限大惩罚。IPO在严格约束下表现优异，但计算复杂度较高。

CRPO（约束修正策略优化）：

在约束违反时交替优化奖励与约束。该方法简单有效，但在某些场景下可能导致策略收敛速度较慢。

FOCOPS（策略空间一阶约束优化）：

在策略空间直接求解约束优化问题，再将解投影回参数空间。FOCOPS理论性能较好，但实现复杂度较高。

实验结果与验证

在实验中，研究人员选择ANYmal C轮腿机器人作为测试平台。目标是在模拟环境中训练感知运动策略，使其能够精准跟踪水平方向的线速度命令以及偏航率命令。为了构建合适的训练环境，研究人员参考并继承了 Rudin 等人提出的四足机器人环境，同时在此基础上设置了多种约束条件。

这些约束条件涵盖关节速度限制（设定为 6.0 rad/s）、扭矩限制（设定为 75 Nm）以及命令平滑度等方面，以此确保训练过程更贴合实际场景，提高策略的实用性和可靠性。在实验的实现与运行方面，所有实验均基于 PyTorch 框架完成，并且在一台配备 NVIDIA GPU 的服务器上运行，以保障实验的高效进行。

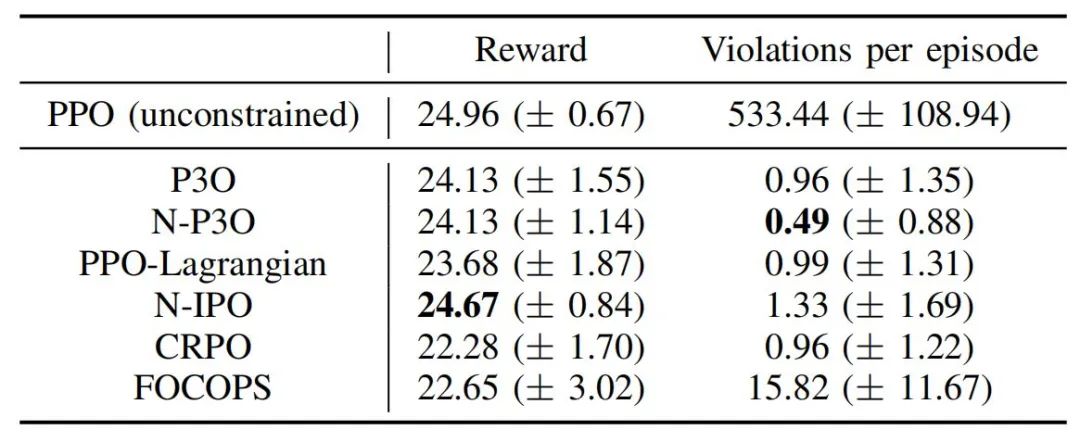
为了探寻最优的算法，研究人员对五种一阶约束策略优化算法在模拟环境中的表现进行了全面比较。经过深入分析，发现 N-P3O（P3O 的归一化版本）算法在约束违反和最终性能这两个关键指标上表现最为出色。N-P3O 算法之所以能够取得如此优异的成绩，关键在于它通过归一化优势函数，巧妙地平衡了奖励与成本优势。这种平衡使得算法在训练过程中能够更快地收敛到稳定策略，并且在测试阶段，其约束违反次数明显低于其他算法。

此外，N-P3O 算法还具备一个显著优势，即对超参数的调整相对不敏感。这一特性大大降低了算法在实际部署过程中的调试难度，提高了算法的实用性和可操作性。

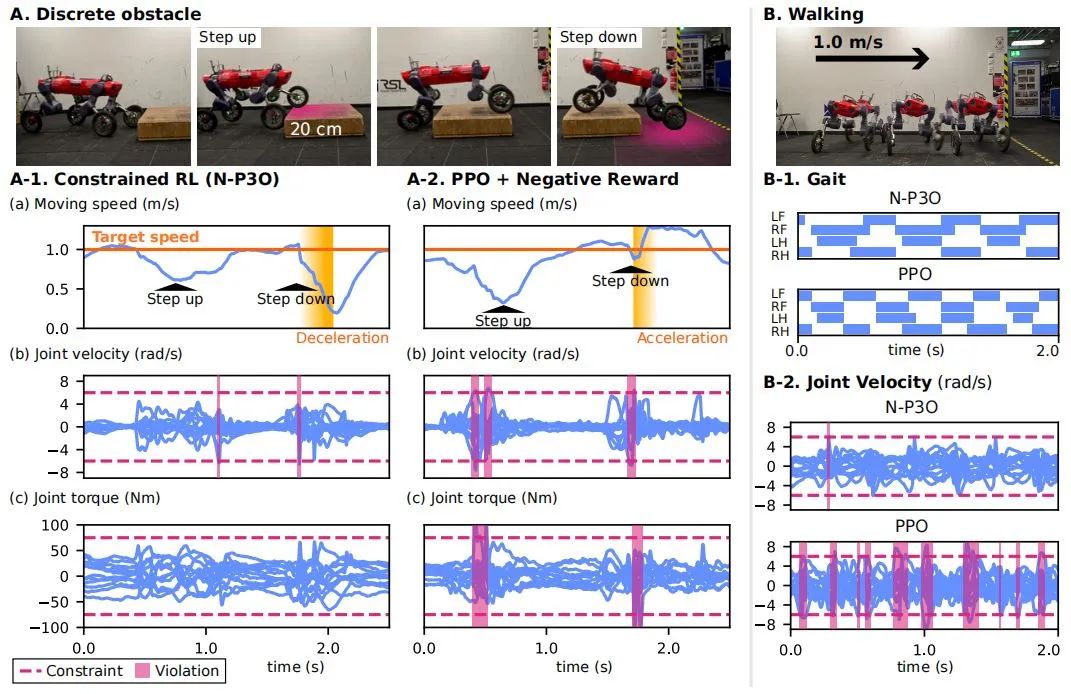
为了进一步验证 N-P3O 算法的实际效果，研究人员在机器人实验中，采用该算法训练的感知运动策略在多种实际场景下进行了测试。这些场景包括穿越离散障碍物以及以最大速度行走等具有挑战性的任务。

实验结果显示，N-P3O 策略在减少约束违反方面表现卓越，同时在轨迹跟踪误差这一关键指标上也优于传统 PPO 策略。特别是在穿越离散障碍物这一复杂场景中，N-P3O 策略展现出了强大的适应性。

它能够主动调整腿部运动和速度，有效减少冲击，从而显著降低约束违反率。与之形成鲜明对比的是，传统 PPO 策略在面对障碍物时，往往采取加速通过的方式，这种策略导致更高的约束违反率和更大的轨迹跟踪误差，进一步凸显了 N-P3O 策略的优势。

结语与未来

约束强化学习借助CMDP框架，把物理约束和奖励函数分开处理，简化了策略优化流程，降低了策略调整难度，还提升了系统的稳定性与安全性。在机器人控制里，物理约束违反可能引发硬件损坏或安全事故，该框架能让机器人在遵守约束的前提下实现高效、安全的运动控制。

在五种一阶约束策略优化算法中，N-P3O算法因约束违反率低、性能稳定而被选为最优。而且，它通过归一化优势函数进一步增强了算法的稳定性和性能。这表明，算法选择和参数调整需综合考虑算法稳定性、性能以及实际应用场景需求。